べん毛モーターの回転計測において，慣性力，遠心力は考慮すべきか？

慣性モーメントで考えてみる

運動方程式から慣性モーメントを考えていきます．

\( \Large \displaystyle m \frac{d^2 x}{dt^2} + \gamma \frac{dx}{dt} \hspace{12pt} [N]\)

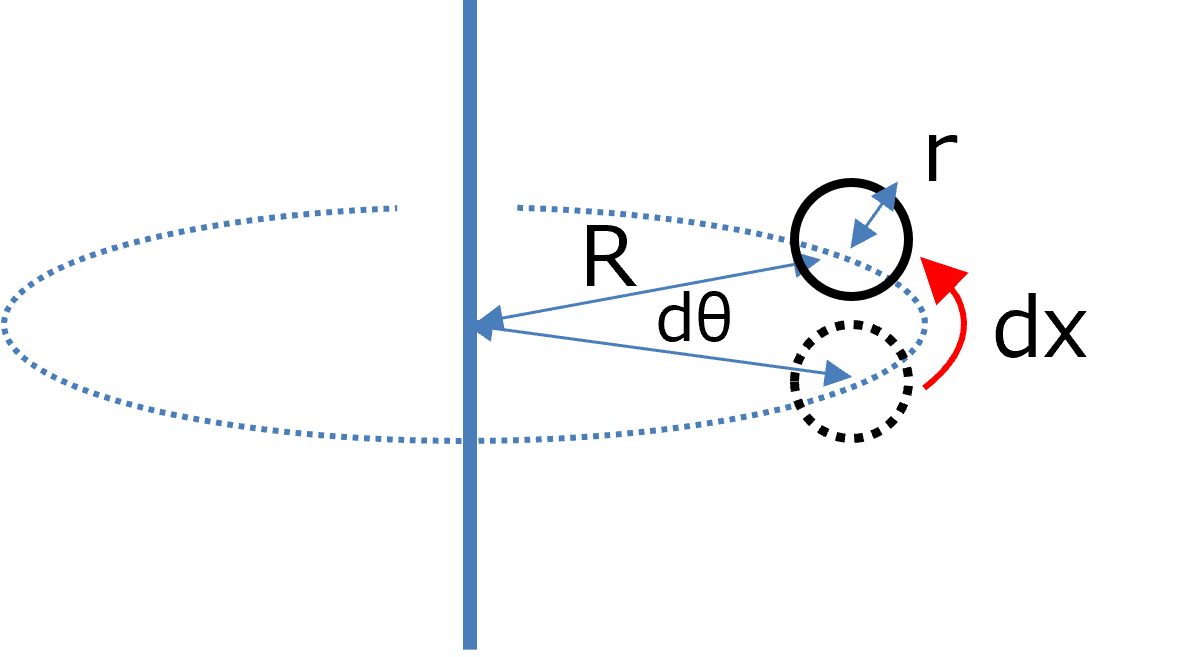
半径Rの円周上を回転する系を考えます．

円周上の変位ｘと変位角θとの関係は，半径がＲの場合，

\( \Large \displaystyle x = R \ \theta \)

\( \Large \displaystyle dx = R \ d \theta \)

\( \Large \displaystyle \frac{dx}{dt} = \frac{dx}{d \theta} \frac{d \theta}{dt} = R \ \frac{d \theta}{dt} \)

\( \Large \displaystyle \frac{d^2 x}{dt^2} = d \left( R \ \frac{d \theta}{dt} \right) = R \ \frac{d^2 \theta}{dt^2 }\)

となるので，

\( \Large \displaystyle m \frac{d^2 x}{dt^2} + \gamma \frac{dx}{dt} = m R \frac{d^2 \theta}{dt^2} + \gamma R \frac{dx}{d \theta}\)

となります．この場合の次元はＮなのでトルクに換算するためにｒを掛けると，

\( \Large \displaystyle m R^2 \frac{d^2 \theta}{dt^2} + \gamma R^2 \frac{dx}{d \theta} \hspace{12pt} [Nm]\)

となると，慣性モーメント，mR²，と粘性項，γR²，との関係（比）=時定数，は，直線の運動方程式と変わらないことになります．

\( \Large \displaystyle \tau \equiv \frac{m}{\gamma} = \frac{m \ R^2}{\gamma \ R^2 } \)

したがって，慣性モーメントは無視してかまわない，という結論になります．

粘性項の係数ですが， 回転粘性抵抗係数，と呼ぶらしいが，あまりネットでは引っかかりません．．．

もっと厳密に計算するには，流体力学，ナビエストークスの法則などを勉強するしかないか．

ここで，慣性モーメントの値，ｍR²，ですが，これは平均軸の定理によるものであり，物体の質量ｍと重心位置と回転中心との距離Rだけで決まるモーメントとなります．

ですので，自分自身の自転による慣性モーメントも考慮しなくてはなりません．

質量ｍ，半径rの球の慣性モーメントは，

\( \Large \displaystyle \frac{2}{5} mr^2\)

公転，自転の粘性抵抗係数は，

\( \Large \displaystyle 6 \pi \eta r \ R^2 , \hspace{20pt} 8 \pi \eta r^3\)

を加える必要があるので，

\( \Large \displaystyle (6 \pi \eta r \ R^2 + 8 \pi \eta r^3) \ \)

となります．ここで，次元は，

慣性モーメント：\( \Large \displaystyle \left( m R^2 + \frac{2}{5} mr^2 \right) \ : \ [Nms^2]\)

回転粘性抵抗係数：\( \Large \displaystyle (6 \pi \eta r \ R^2 + 8 \pi \eta r^3) \frac{dx}{d \theta} \hspace{12pt} \ : \ [Nms]\)

となるので，これらの比＝時定数，を求めることになります．

水溶液中のポリスチレンビーズの運動を考えるので，

\( \Large \displaystyle r = 0.5 \ \mu m = 5 \times 10^{-7} \ [m] \)

\( \Large \displaystyle R = 0.5 \ \mu m = 5 \times 10^{-7} \ [m] \)

\( \Large \displaystyle \rho = 1.05 \left[ \frac{g}{cm^3} \right] =1.05 \times 10^3 \left[ \frac{kg}{m^3} \right] \)

\( \Large \displaystyle \eta = 10^{-3} \ [Pa \cdot s] \)

を使うと，

質量：\( \Large \displaystyle m = \frac{4}{3} \pi r3 \rho = \frac{4}{3} \pi \cdot 1.05 \times 10^3 \cdot ( 5 \times 10^{-7} )^2 = 7.85 \times 10^{-16} kg \)

慣性モーメント：\( \Large \displaystyle m R^2 + \frac{2}{5} mr^2 = 7.85 \times 10^{-16} \cdot 5 \times 10^{-7} \cdot \left( 5 \times 10^{-7} \right)^2
+ 8 \pi \cdot \left( 5 \times 10^{-7} \right)^3
= 1.96 \times 10^{-28} + 7.85 \times 10^{-29} = 2.75 \times 10^{-28} [Nms^2] \)

となり，偏心における慣性モーメントのほうが自転の時に比べて2.5倍ほど大きいことがわかります．

回転粘性抵抗係数：\( \Large \displaystyle 6 \pi \eta r \ R^2 + 8 \pi \eta r^3 = 6 \pi \cdot 10^{-3} \cdot 5 \times 10^{-7} \cdot \left( 5 \times 10^{-7} \right)^2
+ 8 \pi \cdot 10^{-3} \cdot \left( 5 \times 10^{-7} \right)^3 \
= 2.36 \times 10^{-21} + 3.14 \times 10^{-21} = 5.50 \times 10^{-21} [Nms] \)

となり，偏心と自転の粘性抵抗はほぼ同じ大きさとなります．

時定数は，

\( \Large \displaystyle \frac{ m R^2 + \frac{2}{5} mr^2 }{6 \pi \eta r \ R^2 + 8 \pi \eta r^3} = \frac{2.75 \times 10^{-28} [Nms^2]}{5.50 \times 10^{-21} [Nms]} = 5.00 \times 10^{-8} [s] \)

となり，8桁違うので，慣性モーメントの影響はないことがわかります．